
对于发展中国家而言,投资本身是技术进步的最重要方式。
基于索洛模型的增长核算,忽略了资本积累中“嵌入”的技术进步,低估了技术进步对于经济增长的贡献。经验上,亚洲四小龙曾被批评经济增长中要素增加的贡献很大,而技术进步的贡献太小,增长不可持续。但是亚洲金融危机后迅速复苏,保持了高速增长,并进入了高收入国家行列。长期经济发展史上,投资率有一个上升的趋势,美国、德国经济起飞后的投资率远高于经济起飞更早的英国,后来日本在投资率则更高。近年来,印度投资率也随着经济增速大幅上升,超过我国1990年代的水平。对于后发展的国家而言,新增投资中包含了当时先进的技术,并且使用新资本品过程中可以促进人力资本的累积和技术的进步。简言之,对于发展中国家而言,投资本身是技术进步的最重要方式。
1
引言:从索洛模型说起
关于经济增长的一个基本争论,是关于技术进步和资本积累在经济增长中的作用和关系。具体说,到底是技术进步还是资本积累导致了长期经济增长?这二者对于长期增长的含义有何不同?这二者之间的关系又是什么?是两个独立的过程还是交互的过程?如果是交互的过程,那么是技术进步导致了资本积累,还是反过来?对于发展中国家还要问,这种关系在发达国家与发展中国家是基本相同,还是有显著不同?正确回答这些问题对于理解我国的高投资率在经济发展中的作用,对于未来经济形势的判断,以及政策制定,都具有基础性的意义。
罗伯特·索洛(Robert Solow)在1956年创立的索洛模型,是研究经济增长的基准模型,对后来的理论与实证研究,都产生了深远的影响。[2] 这一模型把经济增长归结为要素增长和技术进步,推导出稳态的增长路径和决定参数,提供了一个描述和理解经济增长的可操作的参照系统。后来的经济增长模型,包括内生增长模型,都是在索洛模型的基础上进行改进和扩展。[3]
简而言之,索洛模型把产出写成资本和劳动的函数:
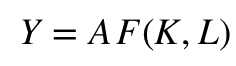
其中,K代表资本,L代表劳动,A代表生产技术,给定资本和劳动投入,产出随着A的提高而增加。文献中经常使用的柯布-道格拉斯(Cobb-Douglas)生产函数,即
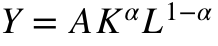
具有边际收益递减,规模报酬不变,资本与劳动的收入份额不变等重要性质,这些性质给建立和推导模型带来很大便利,也可以帮助描述、概括一些常见的增长特征。
索罗模型的一个重要应用,就是利用增长核算(Growth Accounting)的方法对经济增长进行分解,也就是把经济增长分解为“要素投入增加”和“技术进步”两部分,前者包括劳动人口的增加、人力资本的增加、资本的积累,后者包括科学技术知识的进步、规模经济、资源配置效率的提升等等。[4]
这一分解的意义在于分析经济增长的来源。倘若一个经济的增长仅仅依赖于投入的增加,而不是技术进步,那么这种增长将是不可持续的。原因很简单,任何一个经济的要素资源都是有限的,特别是劳动力资源是有限的,要素投入不可能无限增加。更重要的是,要素投入增加还受到边际收益递减的约束,无法成为持续的经济增长的源泉。相反,技术进步可以是无限的,而且不受边际收益递减的约束。索洛模型的一个重要贡献,就是清晰说明只有技术进步才能维持长期的、持续的经济增长。
索洛模型的这一含义,被广泛接受和传播,对于人们观察和思考经济增长,有着深远的影响。比如说,我国的投资一直增长很快,远快于GDP的增长,投资占GDP的比重也很大,且有上升的趋势(图1),近年来接近GDP的差不多一半,引发投资是否过度,经济增长是否能够持续的争论和担心。这一争论对于思考未来的经济增长和政策制定有着方向性的意义。
图1:资本形成总额占GDP的比重(1978-2017)
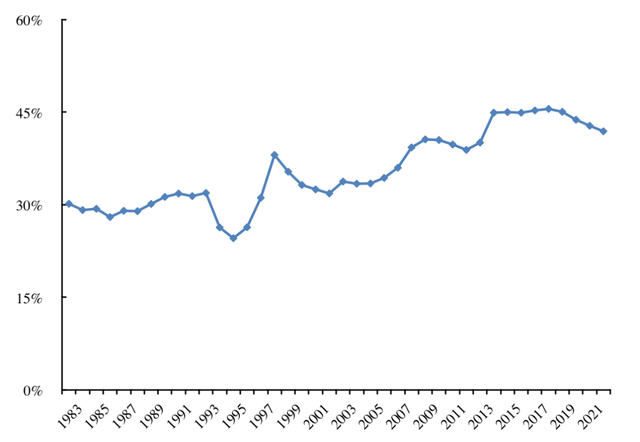
数据来源:历年《中国统计年鉴》。
再比如,亚洲四小龙虽然保持了长期的高速增长,但是也没能逃脱增长主要依靠要素累积,技术进步贡献很少的批评。在1990年代,特别是在亚洲金融危机以后,四小龙的增长模式受到很多批评。这些担心和批评无疑是合理的、重要的,但是事关对于未来经济增长的判断,事关基本的经济政策导向,还是要大胆批评,小心求证。经济分析虽然并不复杂,却往往是“差之毫厘,谬以千里”的。[5]
[1] 本文原是作者在反思中国经济发展,特别是投资在其中的作用时的笔记,缘起在于目前对“过度投资”的批评意见很多,但是投资又确实带来了经济增长和技术进步。整理成文过程中,为了行文的简明和流畅,没有加入太多理论推导和技术性注解。本文亦没有尝试做系统全面的文献综述,而只是选择性引用一些相关的文献,特别是与投资和技术进步的讨论有关的文献。毕竟,对于经济增长的优秀教科书和文献综述已经很多。整理成文的另一个动因,是在北京大学讲授经济增长期间,觉得一些话可能没有说很清楚,因而也需要对学生有一个补充交代。
[2] 几乎与索罗同时创建索洛模型的是Swan。在索洛模型中,储蓄率是外生的,后来Cass和Koopmans等人引入家庭的最优决策,把储蓄率内生,拓展了索洛模型,因而索洛模型也被称作Solow-Swan-Cass-Koopmans模型。相关文献参见R. Solow, “A contribution to the theory of economic growth,” Quarterly Journal of Economics, vol.70, no. 1, 1956, pp. 65–94. T. Swan, “Economic growth and capital accumulation,” Economic record, vol.32, 1956, pp. 344-61; D. Cass, “Optimum Growth in an Aggregative Model of Capital Accumulation,” The Review of Economic Studies, vol. 32, no. 3, 1965, pp. 233-240; T.C. Koopmans, “On The Concept of Optimal Economic Growth”, in The Econometric Approach to Development Planning, Amsterdam: North-Holland, pp. 225-195.
[3] 代表性的内生增长模型包括模型,参见K. J. Arrow, “The Economic Implications of Learning by Doing,” The Review of Economic Studies, vol. 29, no. 3, 1962, pp. 155-173; M. Frankel, “The Production Function in Allocation and Growth: A Synthesis”, The American Economic Review , vol. 52, no. 5, 1962, pp. 996-1022; P. M. Romer, “Increasing Returns and Long-Run Growth,” Journal of Political Economy, vol. 94, no. 5, 1986, pp. 1002-1037. R. E. Lucas, “On the mechanics of economic development,” Journal of Monetary Economics, vol. 22, no. 1, 1988, pp. 3-42.;产品多样性模型,参见P.M. Romer, “Growth Based on Increasing Returns Due to Specialization,” The American Economic Review, vol. 77, no. 2, Papers and Proceedings of the Ninety-Ninth Annual Meeting of the American Economic Association, 1987, pp. 56-62; P.M. Romer, “Endogenous technological change,” Journal of Political Economy, vol. 98, no. 5, 1990, pp. 71–102.;和熊彼特类型模型,参见P. Aghion and P. Howitt, “A model of growth through creative destruction,” Econometrica, vol.60, 1992, pp. 323-351。
[4] 增长核算首先由Solow本人提出,并对后来对增长的实证研究产生了重要的影响,成为理解经济增长的一种重要方法,参见R. Solow, “Technical change and the aggregate production function,” Review of Economics and Statistics, vol. 39, no. 3, 1957, pp. 312–20。早期的代表性文献还包括J.W. Kendrick, “Front matter, Productivity Trends in the United States,” NBER working paper, 1961.E.F. Denison, The Sources of Economic Growth in the United States and the Alternatives Before Us, Washington, DC: Committee for Economic Development, 1962. D. W. Jorgenson and Z. Griliches, “The Explanation of Productivity Change,” The Review of Economic Studies, vol. 34, no. 3, 1967, pp. 249-283。近年来,应用增长核算的方法理解亚洲经济增长引起了广泛争议,参见A. Young, “The Tyranny of Numbers: Confronting the Statistical Realities of the East Asian Growth Experience,” Quarterly Journal of Economics, vol. 110, no. 3, 1995, pp. 641-80; A. Young, “Gold into Base Metals: Productivity Growth in the People’s Republic of China during the Reform Period,” Journal of Political Economy, vol.111, 2003, pp. 1220-1261; C.T. Hsieh, “What Explains the Industrial Revolution in East Asia? Evidence From the Factor Markets,” The American Economic Review, vol. 92, no. 3, 2002, pp. 502-526.
[5] 经济现象的两个重要特点导致了方法论上的困境。其一,人们都具有一定的经济常识,因而经济分析看起来是一个进入门槛很低的行业。然而,经济现象和所有的社会现象一样,其实非常复杂,影响因素很多,必须充分积累,全面观察,才能得到较为全面的理解,进行较为准确的分析。只掌握部分的观察,或者有意无意忽略一些重要的方面,往往导致片面的解读甚至误导。其二,数理方法的运用大幅推动了现代经济分析,对经济学的进步做出了重要的贡献。然而,数理方法的一个难点是有些重要的因素难以量化而被忽略,导致分析结果可能产生偏差。另外,数理方法抽象掉了一些重要的对真实世界的观察,这本身无可厚非,因为每一种方法都有所侧重。但是,需要把抽象掉的重要观察补回来,结合使用数理方法和经验观察,才会有较好的分析和结论,否则也容易导致偏差和误导。
2
增长核算遗漏了什么
还是从索洛的经典分析说起。在索洛模型中,以及后来的拓展中,技术进步由一个独立的参数(经常用字母A指代)来表示,或者外生,或者内生,但是与资本积累都是分开的。这里面不甚清楚的是,技术进步在现实经济中是如何体现的?理论分析中,可以用一个参数来表示技术进步,这样数学上也很好处理。然而,现实中的技术进步,却不仅仅是一个抽象的参数,而是要有实实在在的载体的。
新技术的有效应用,和几个关键的要素是联系在一起的:1)新的机器设备,比如说新的炼钢技术,需要对应的一整套设备;2)辅助新技术、新设备、新产品的基础设施,比如说,没有便利的交通,无论什么产品也运不出去,也就谈不上打开市场了;3)新的生产要素的采用,比如说,农业技术的进步,与不断改进的化肥,农药,种子的发明和改进是分不开的;4)具有使用新要素,操作新机器的人,这里面不仅需要基础教育,还需要专业培训;5)与新技术、新的生产方式相适应的、新的生产组织方式。
上面这五大要素,大都是需要投资的,包括固定资产投资、研发投资、人力资本投资。然而,在增长核算当中,其中很大部分的投资,包括全部固定资产投资和研发投资,都是算入资本积累的。[6] 由于技术进步在增长核算中是扣除所有要素增长后的残差,因而这些记入投资的项目都增加要素积累的贡献,同时减小技术进步的贡献。[7]

需要追问的是,倘若没有这些投资,技术进步如何实现?实验室里的成果,最终是要固化在机器设备中的。新的生产要素,人力资本所代表的技能,也是要和恰当的机器设备结合才能带来生产力的。没有这些投资,技术进步是无法与经济增长结合的。这一层讨论的含义是,投资既带来资本积累,也体现了技术进步。根据索洛模型进行的增长核算,可能忽略了资本积累中包含的技术进步,因而低估了技术进步的贡献。
[6] 人力资本投资大部分情况下不计入投资。家庭的学校教育支出是计入消费的,企业的培训支出一般也不计入投资,公共支出中的教育支出也不计入投资。倘若这些支出计入投资而形成人力资本,那么资本存量将增加,索洛残差将减小。
[7] 在增长核算中,要素增加是从国民经济统计中直接核算出来的,从经济增长中扣除要素增加的贡献,就得到技术进步的贡献,因而,技术进步也被称作“索洛残差”。因为增长核算并不直接计算“技术进步”,而只是用一个残差项来替代,因而讨论中也称之为“对于经济增长的原因的无知”,参见M. Abramovitz, “Resource and Output Trends in the United States Since 1870,” The American Economic Review, vol.46, no.2, 1956, pp. 5-23。
3
回首亚洲金融危机
不同增长路径下的“技术进步”
一个典型的例子,就是著名经济学家保罗·克鲁格曼(Paul Krugman)关于“亚洲无奇迹”的著名论断。1994年,克鲁格曼在《外交事务》(Foreign Affairs)杂志发表题为《亚洲奇迹的神话》(The Myth of Asia’s Miracle)的文章,分析韩国、台湾、香港、新加坡这亚洲四小龙的增长因素,发现东亚国家的经济增长靠的主要是要素投入的增加,也就是高劳动参与率、高储蓄、高投资,而非技术进步。因为要素投入总有限度,而且边际产出递减,在这一证据基础上,克鲁格曼做出了“亚洲无奇迹”的著名论断,并预言“亚洲奇迹”难以持续。[8]
克鲁格曼是一个雄辩的写手,在前苏联刚刚解体、东欧国家刚刚发生剧变的背景下,他把亚洲四小龙与前苏联类比,指出二者的共同之处在于经济增长当中都没有技术进步,确实让人猛然警醒。在克鲁格曼的眼里,亚洲四小龙和前苏联一样是“纸老虎”,无法对西方发达国家的经济地位形成威胁。把经济增长问题置于国际竞争的语境下讨论,亦增加了克鲁格曼文章的影响。
克鲁格曼无疑是幸运的,他在亚洲金融危机爆发之前做出了这一论断,随着亚洲金融危机的爆发,他声名鹊起,被认为是“成功预测了”亚洲金融危机的人。
克鲁格曼的这一预言,为部分观察研究中国经济发展的人津津乐道,还有一个重要的原因,就是我国的经济增长也严重依赖投资,比起亚洲四小龙等国家有过之而无不及。克鲁格曼对亚洲四小龙的批评,对我国也毫无疑问是适用的。近年来讨论中,对于我国投资过高的批评,也是不绝于耳。
然而,将近二十年以后,回头再看克鲁格曼的批评,值得商榷之处颇多。首先,哪一个经济体不经历经济波动?发展中国家的经济发展波动很大,期间不乏大起大落,拉美国家的经验就是明证。即便是美国也经历过大萧条,而且大约每10年就经历一次经济衰退,大约每30年经历一次大的经济危机,但是似乎没有人说美国的经济增长没有技术含量。毕竟,经济周期和经济增长是两个问题,不能拿经济波动现象来讨论经济增长。
其次,亚洲金融危机以后,这些经济体的表现明显超过世界平均水平。表1比较了2000-2017年东南亚、发达国家、和世界平均经济增长速度,发现东亚国家的增长速度还是要快得多,大约有4.79%,而世界平均只有2.89%,东亚国家比世界平均快了超过1.9个点,比高收入OECD国家更是快了超过3个点。为了剔除2007年以来美国次贷危机和全球金融危机的影响,表1进一步比较了2000-2007年的情况,发现大致同样的结论。熟悉经济增长的人应该很了解的是,2-3个百分点的差别,可是非常大的。在20世纪以前,超过1%的经济增长,被广泛认为是不可能的。再举个例子来说,倘若欧美经济增速多出两个点,那么主权债务就会很容易被经济增长消化掉,就不会有那么多人讨论欧洲债务危机了,甚至不会有“欧债危机”这个词。
表1:亚洲金融危机后的东南亚和世界经济增长
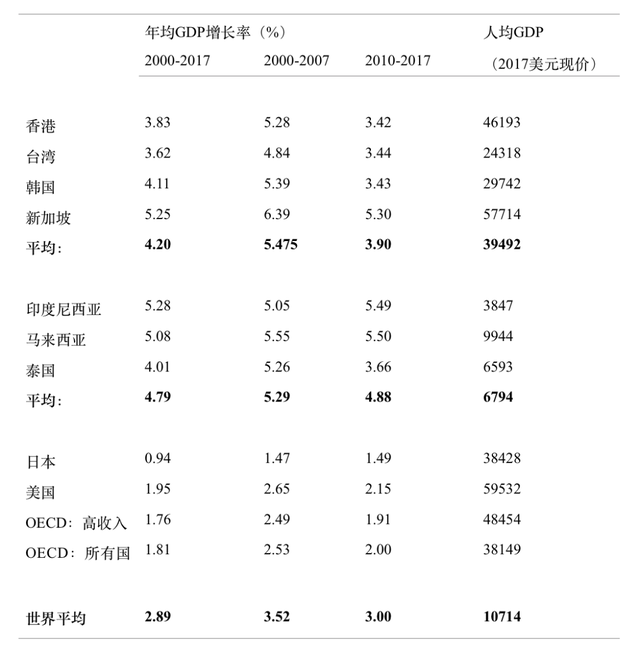
数据来源:台湾数据来自台湾统计局,其他国家(地区)数据来自世界银行的世界发展指标(World Development Indicators,WDI)数据库。
需要指出的是,随着经济的进一步发展,一些国家的科技进步也在提升,产业也在迅速升级当中。比如说韩国,在金融危机以后迅速恢复,十年间的平均增速达到5.16%,人均GDP达到2万美元以上,而且韩国在电子、汽车等产业的技术进步是有目共睹的。比如说,现在的三星电子产品的质量已经受到广泛赞誉,可以和日本的高端电子产品在世界市场上竞争。
最后,倘若拉长历史的视角,二战以后很少有国家(地区)能够保持长时间的高速增长,跨越中等收入陷阱,步入高收入国家行列。除去富于石油等自然资源的国家,亚洲四小龙是为数不多的例外。从这个角度讲,四小龙是无愧于“奇迹”一词的。
然而,我们依然还需要回答一个问题,就是为何根据同样的增长核算方法,发达国家经济增长中技术进步的份额要大很多,而亚洲四小龙却要小很多。根据著名增长经济学家罗伯特·索洛、爱德华·丹尼森(Edward F. Denison)等人的计算,美国的经济增长中,大约只有八分之一归因于资本积累,四分之一归因于人口增加,六分之一归因于教育水平提高,剩下的大约50%归因于资源配置优化、规模经济、知识积累等因素,而这些都归入广义的“技术进步”。
作为比较,根据另一位增长经济专家阿伦·扬(Alan Young)的仔细计算,亚洲四小龙的增长中技术进步的贡献要小得多,其中香港好一些,但也只有30%,台湾和韩国分别只有28%和17%,而新加坡的技术进步的贡献只有2%,只考虑制造业的话甚至是负数。这些人都是严谨的学者,他们的计算结果值得仔细揣摩。
其中新加坡的情形比较极端,也很有启发性。根据阿伦·扬的计算,1970-1990二十年间,整个经济增长中技术进步的贡献几乎为零,只考虑制造业的话甚至为负。然而,很难相信新加坡二十年的经济增长中没有技术进步的贡献。何况,新加坡的增长速度、人均收入在亚洲四小龙中是最好的,很难相信技术进步贡献最小的国家最后表现最好。
举一个简单的例子。假设新加坡做的是最简单的加工制造,为了扩大生产而买了一台新型设备,可以大大增加生产能力,大大提高劳动生产率。根据增长核算,这是一笔投资,是不计入技术进步的。然而,这种方法没有考虑新型设备中包含的新技术,也没有考虑新设备带来的生产中进行的所有人力资本积累。实际上,新技术总是要体现在新的机器设备,或者其他生产要素当中的,否则新技术如何进入生产?

上面的例子说明传统的增长核算低估了技术进步对于经济增长的贡献。倘若如此,依然有一个问题需要回答,就是为何这种低估在亚洲四小龙比在美国要大得多?毕竟方法是一样的,如果低估的程度是一样的,就依然不能解释上述差别。
其实这不难理解。发达国家处于科技的前沿,在发展过程中需要不断研发,而且在漫长的发展过程中,不断提高教育投入。在此期间,物质资本逐步积累,人力资本也逐步增加,技术水平逐步进步,资源配置方式慢慢变化,生产组织效率逐步提高。在这个过程中,资本积累的速度比较慢,而且由于时间跨度大,折旧也比较多,而技术水平、资源配置方式、生产组织效率的提高,都会反映在“索洛残差”当中,被增长核算解读为广义的技术进步。
相比较而言,东亚国家是后发国家,主要利用、改进现有技术,在短时间内通过购买现成的设备,提升基础设施来吸收、利用现有技术,并且和受过良好基础教育的劳动力人口进行结合,配套引进生产组织方式。这样,东亚国家的经济增长,更多地表现在投资增长上,并不奇怪。各国发展路径不同,表现出不同的特征也是自然的,理应进行具体分析,而不是强求简单雷同。[9]
克鲁格曼在贸易领域卓有建树,并因此获得诺贝尔经济学奖,其经济学造诣毋庸置疑。然而克鲁格曼对于增长核算的应用,却值得商榷,至少在细节上值得商榷。然而,细节决定成败,经济分析往往是差之毫厘、谬以千里的。特别值得反思的是,我们对于投资在经济发展中的作用,是否有一些偏见?对于研究经济增长的学生来说,还要进一步反思已有模型的缺陷,或者对已有模型的误读,以及产生的误导。
[8] P. Krugman, “The Myth of Asia’s Miracle,” Foreign Affairs, vol.73, no. 6, 1994, pp. 62-78.
[9] 关于东亚经济增长模式的争论,参见:E. Chen, “The total factor productivity debate: determinants of economic growth in East Asia,” Asian-Pacific Economic Literature, vol. 11, no. 1, 1997, pp 18-38;郑玉歆:《全要素生产率的测算及其增长的规律——由东亚增长模式的争论谈起》,《数量经济技术经济研究》,1998年第10期,28-34页;林毅夫、任若恩:《关于东亚经济增长模式的再讨论》,《经济研究》2007年第8期。
4
发达国家早期的“过度投资”
在反思了有关亚洲四小龙的争论以后,我们可以进一步把历史的广角镜继续往前倒推。四小龙的经济增长被批评依赖要素投入,特别是高投资,那么在发达国家早期的历史上是不是也有投资过高的批评?早期的资本、劳动力、教育等各种数据比较难以获得,有的数据的质量也值得担忧,计算全要素生产率比较困难,因此我们主要看发达国家的历史上是否也存在“过度投资”。
工业革命以来,英国、荷兰率先经济起飞,比利时、法国等其他欧洲国家紧接其后,然后美国、加拿大等先后接过了经济起飞的接力棒,二战以后则是日本等国家。换一个角度来看,相对于更早起飞,当时已经相对“发达”的英国、法国等国家,美国、加拿大、日本等国家在历史上的一些时段都可以看作是“发展中国家”。此外,二战以后的重建时期,很多受到战火破化的国家收入水平低于战前,但是世界的技术进步并未停止,这些国家也可以看作是“发展中”国家。这样,倘若我们上文的逻辑正确,应该观测到一种趋势,就是从英国、法国到美国、澳大利亚、日本,我们应该观测到投资率的上升。也就是说,在美国高速发展的阶段,其投资率应该比早期的英国高很多,而后来日本的储蓄率应该比美国高一些。
搜集整理经济发展的早期历史,看起来证据支持这种猜测,表2总结了一些代表性发达国家早期的投资率。1780年以前,英国投资率只有5%左右,到了1870年的投资率也不到10%,其后的投资率大致稳定在这一水平,一直不太高,二战以后的恢复时期也只有16%。相对于英国,经济起飞稍晚一点的意大利、丹麦、挪威、瑞典等国家的投资率要高一些,一战以前达到了15%左右的水平,大约比英国提高了5个百分点。
从大约1870到一战爆发以前的四十多年时间里,德国、美国、加拿大的经济发展很快,人均收入都翻了一番还要多,而英国、意大利等国只增长了大约50%。相应地,德国、美国、加拿大的投资率也进一步上升,达到20%左右,比意大利、丹麦、挪威、瑞典等国家又上升了5个百分点。
从1914-1945年间,世界经历了两次世界大战,其间大部分国家的投资率有所下降,比如英国、德国、美国、加拿大,但是也有例外,比如意大利。二战以后的重建时期,大部分国家的投资率有明显上升,除英国外都达到了20%以上,其中挪威达到了30%左右。二战以后经济起飞的代表是日本,投资率达到30%,这已经是大家很熟悉的情况。
表2:发达国家(地区)与新兴发达经济体早期的投资率
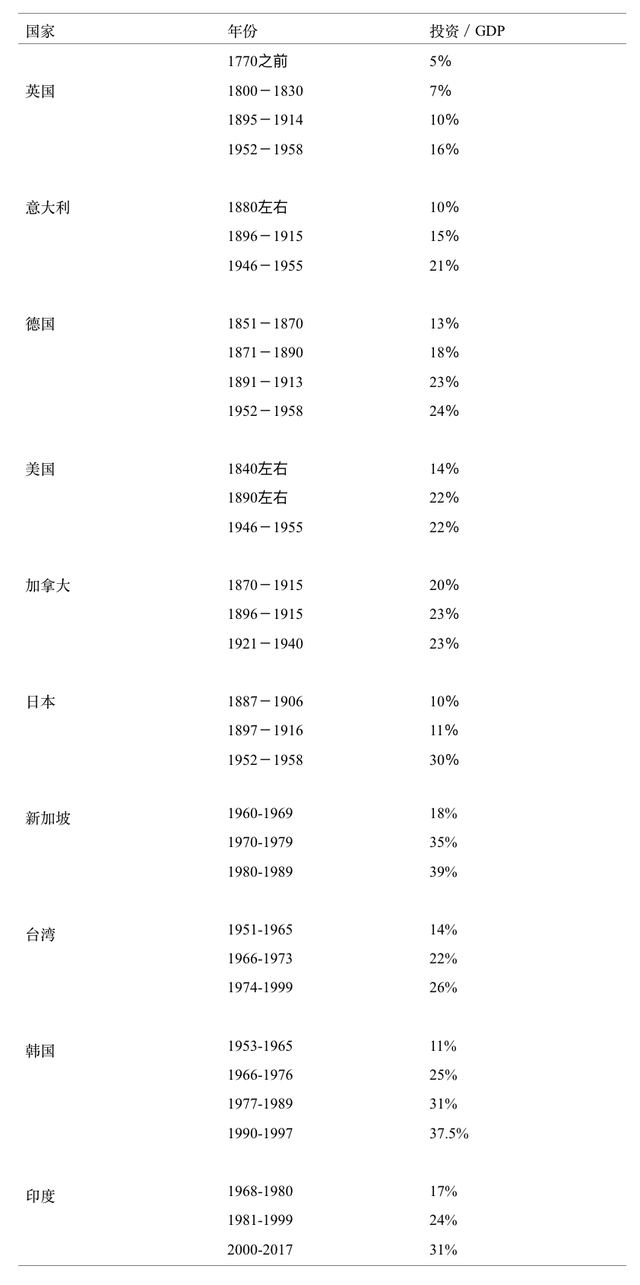
数据来源:发达国家数据摘自S. Kuznets, “Quantitative Aspects of the Economic Growth of Nations: VI. Long-Term Trends in Capital Formation Proportions,” Economic Development and Cultural Change, vol. 9, no. 4, 1961, pp. 1- 124.为简明计,合并了一些年份,并省略了两次世界大战期间及其中间的数据。新兴经济体数据来自于新加坡统计局、台湾统计局、韩国央行及世界银行的世界发展指标(World Development Indicators,WDI)数据库。
从1760到1960年代这大约200年的时间,是世界经济发展的分水岭。在此之前,世界经济的增长很缓慢,东西方的差距也不大。在这200年期间,欧洲完成工业革命,成为经济比较发达的国家。而进一步细看这200年,我们发现经济起飞早、增长时间长、速度慢的国家的投资率要低一些,而经济起飞晚、增长时间短、增长快的国家的投资率要高一些。直观上这其实很好理解,后起国家直接利用先进技术,短时间内需要购置更多设备,收入的增长浓缩在更短时间里,投资率自然高一些。
一个有意思的问题是,当初德国、美国、加拿大等国家的投资率远高于当时的发达国家英国,更加远高于英国历史上的投资率,不知当时有没有很多“过度投资”的热烈争论?倘若有,不知事后人们怎么看。
图2:印度的投资、制造业和净出口(占GDP%,1968-2017)
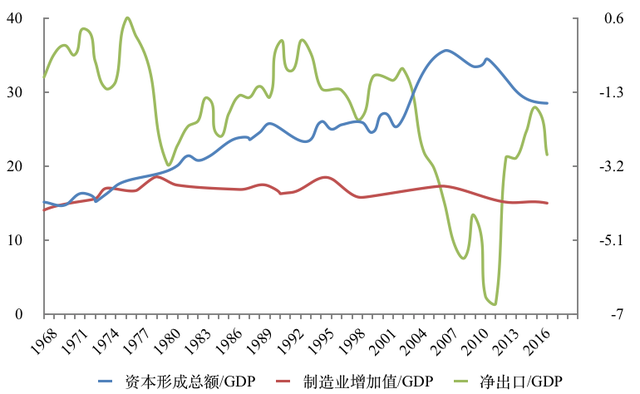
数据来源:世界银行世界发展指标(World Development Indicator, WDI)数据库。净出口坐标在右轴。
近年来印度的经验也很有意思。我国的学者时常喜欢把中国与印度作比较,因为印度和我国既有人口总量、幅员面积等方面的可比性,又有很多不同,比如政治制度、宗教传统、经济结构等方面。传统上,印度的投资率一直不是很高,新世纪以前基本在25%以下(图2)。可是进入新世纪以来,印度经济增长的加速伴随着投资率的大幅上升,2004年以来达到30%以上,2007年来更是达到了35%以上。按照“传统”的国际比较,这也是高得异常的投资率。别忘了,现在印度的人均收入还只有1500多美元,可比价格计算相当于我国1990年代中后期的水平,而那时我国的投资率还不到35%,低于现在印度的投资率。随着印度经济的进一步发展,印度的投资率有可能会进一步上升,会不会向我国一样达到45%以上,让我们拭目以待。
需要指出的是,印度的经验也帮助撇开一些容易引起混淆的因素。首先,印度的服务业相对很发达,但是制造业并不发达,制造业增加值占GDP的比重不到15%,但是投资率依然可以很高,说明投资率和制造业虽然相关,但并不是必然的关系。倘若印度的制造业更发达,投资率有可能还要高一些。第二,印度大多数年份是一个净进口的国家,说明投资率高和净出口也没有必然的关系。净出口相当于国内在国外的净储蓄,净出口多的话,意味着国内的储蓄超过了国内的投资而已。在国内投资需求受到资金约束的情况下,投资率会因为储蓄的增加而增加,净进口不过是利用了国外的储蓄而已。
5
反思增长模型
上述理论分析,以及对于历史和近年来的国际经验的讨论,都表明增长核算方法低估了投资对于技术进步和长期经济增长的作用,且低估的程度在处于落后、学习地位的发展中国家可能要大一些。一个重要的渠道,是落后国家可以通过投资吸收采用先进技术,促进技术进步,以及人力资本的积累。
实际上,文献中对于这一问题早有探讨。增长核算方法的创始人,同时也是索洛模型的创立者,罗伯特·索洛本人早在1960年,就提出了投资当中蕴涵着技术进步的观点,并命名为“嵌入式技术进步”(embodied technology progress),也就是说技术进步是“嵌入”在资本形成当中的。[10] 后来的研究也试图在增长核算中考虑这一因素,对增长核算进行调整。然而,调整的结果却远不如人意。例如,一种主流的方法倾向于用投资价格指数修正实际投资,由于投资品价格趋于下降,这一方法实际上夸大了投资的贡献,进一步减小了技术进步的贡献。
索洛引入了“嵌入式技术进步”这一重要概念,但是同时也产生了新的问题。索洛意义上的嵌入式技术进步,只考虑了资本累积过程本身的技术进步,也就是生产资本品的成本减少,但是没有考虑新的资本品蕴涵了新的技术和生产能力。准确而言,索洛意义上的“嵌入式技术进步”,表达的是生产资本品需要的投入的减少,也就是生产每一个单位的资本品(比如机器设备)耗费的资源减少,这实际上是资本品部门相对于消费品部门的技术进步,或者称之为“相对技术进步”,而不是“总体技术进步”。
在古典索洛模型的抽象世界里,只有一个消费品,并且资本品是从消费品转变而来的,这时资本品部门的“相对技术进步”其实也反映了一些“总体技术进步”的成份。实际上,在这一简化的世界里,消费品是“计价物”,资本品可以视为存储和(扩大)再生产消费品的一种设备。生产资本品消耗的消费品的减少,其实可以看作是“存储技术”的进步,并可以进一步看作是生产消费品的技术的进步。从这个角度理解,“相对技术进步”也包含了一般性的生产技术的进步。
然而,“相对技术进步”与“总体技术进步”依然不同。即便在最简单的索洛模型中,资本依然要和劳动结合来生产,制造最终产出,这一过程中体现在“生产函数”当中。生产函数的变化,是索洛意义上的“嵌入式技术进步”无法体现的。比如说,人们研发出一种新的技术,可以大幅提高产出,这种技术体现在一种新的设备(以及与设备配套的能力)当中。这种新设备可能耗费很多资源,也可能耗费很少资源,但是其代表的生产能力与生产设备耗费的资源数量是两个维度的概念。索洛意义上的“嵌入式技术进步”只能体现后者,而不能体现前者。举一个例子,现在的电子计算机质量越来越好,价格越来越便宜,这是生产计算机的技术进步的结果,但是计算机普及使用能够带来的技术进步,却是另外一回事情。

可见,索洛(1960)年倡导的“嵌入式技术进步”,其实只是狭义的技术嵌入,而广义的技术嵌入,需要考虑新的资本中蕴涵的新的生产技术。在数学表达上,索洛意义上的技术嵌入只考虑了总生产函数:
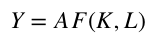
中K的累积方式的变化,而没有考虑其实生产技术 应该是资本 的函数。这样生产函数就可以写作:
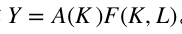
这样的生产函数能够表达广义的“嵌入式技术进步”的思想,但是随之而来也带来了数学处理上的变化。比如说,常用的Cobb-Douglas的生产函数就不再适用了,因为如果生产技术 是资本 的函数,如果不对这个函数形式加以约束,那么总体生产函数的形式就应该是不断变化的。理论上,我们可以对 的形式加以约束,使得总体生产函数依然保持类似于Cobb-Douglas函数的形式。最简单情形,假设 是 的指数函数(当指数为1时退化为线性函数),而 依然是Cobb-Douglas形式,那么总体生产函数依然是指数形式,但是资本项的指数变大,而且指数的和要大于1。但是此时的一个重要变化是,当Cobb-Douglas生产函数的指数和大于1,如何进行增长核算?如果进行惯常的增长核算,会产生什么样的结果?应该进行什么样的修正?应该如何解读?
但是在生产函数的指数和大于1的情况下,如果一定要进行增长核算,需要给资本项一个大于常见的资本份额的指数(也就是资本累积对经济增长的贡献的权重),这时会减小索洛残差。倘若这个指数足够大,那么索洛残差项可以达到零,甚至小于零。背后的经济逻辑是,由于技术进步的外部性,以及技术进步嵌入在资本累积当中,资本累积也具有“外部性”,或者称为“溢出效应”。倘若继续按惯常的方法赋予权重,则资本中包含的技术进步的贡献没有考虑,索洛残差被高估。
这里可能有一点奇怪,就是考虑了嵌入式技术进步以后作为“技术进步”的代表的索洛残差会进一步减小。理解这一点的切入点在于,如果我们考虑了所有的因素而没有遗漏,索洛残差理论上应该为零。索洛残差之所以大,就是因为我们遗漏的多。现在我们少遗漏了一项,嵌入在资本积累中的技术进步,因而索洛残差变小了。
回到新加坡的例子。根据Young(1995)的核算,新加坡的增长中技术进步的成分很低,无非说是索洛残差很低。其实这不难理解。作为一个具有启发意义的比方,不妨把新加坡经济简化理解为把几个先进的工厂搬到一个岛上,经济生活的其他方面都不发生变化,经济增长体现为这几个工厂的产出的增长。这种情况下,工厂雇用的资本和劳动力可以完全解释工厂的产出的增加,因而没有留下太大的残差。一定要找残差的话,不妨把这些工厂的利润当做是残差,因为利润是支付了生产成本、资本和劳动收入份额之后的剩余。现实中我们知道新加坡政府的主权基金数目可观,反应新加坡企业的利润不菲。[11] 从这个角度看新加坡经济并非没有“索洛残差”,而是有很大的索洛残差。相比之下,香港、台湾、韩国等经济体的较大的索洛残差 [12] ,更多反映了这些经济体的经济组织的变化。这些经济体比新加坡大许多,经济组织形式复杂许多,新加坡那样简单地可以用几个先进工厂来等价。当然,这些都是一个程度的问题。
如此修改生产函数的情况下,对于索洛残差的解释也要发生一点变化。首先,这时候索洛残差的概念不一样了,我们不能再说索洛残差是技术进步,至少不能是全部的技术进步,因为部分的技术进步已经在资本积累中体现了。其次,我们甚至也不能说索洛残差是我们对经济增长的无知。一个更准确的说法,是索洛残差是我们对于经济增长的无知的部分,我们知道的部分,已经被分解出来了。最后,把索洛残差解读为“总要素生产率”(Total Factor Productivity,简称TFP),容易产生误导,也与拓展的生产函数不符合,不妨考虑放弃这种解读。
有一点无论如何应该明确,那就是增长核算的目标,本来就不应该是寻找一个大的索洛残差,而是达到尽量小的索洛残差。理想状况下,如果考虑了所有的增长贡献因素,索洛残差应该等于零。
[10] R. Solow, “Investment and technological progress,” in K. Arrow, S. Karlin and P. Suppes, eds., Mathematical methods in the social sciences 1959, Stanford, Calif.: Stanford University Press, 1960, p.89–104.
[11] 根据美国主权财富基金研究所(Sovereign Wealth Fund Institute)的统计,到2012年,新加坡的主权债投资基金为2475亿美元(http://www.swfinstitute.org/fund-rankings/),这一数字与与新加坡的年度GDP相当。
[12] 把利润等同于索洛残差只是一个比喻的说法。一个重要的区别是利润去除了利息,但是包含了自有资本的回报,因而利润实际上包含了资本的收入份额和索洛残差两个部分。
6
内生增长理论与“嵌入式技术进步”
索洛模型假定技术进步外生,后来的内生经济增长理论把技术进步内生了,从而拓展了索洛模型 [13]。这些内生增长模型,把技术进步内生了,但是对于资本积累与技术进步的关系,特别是嵌入式技术进步的理解,并没有投入太大的注意力。
当然,新的资本品中包含着新技术这一点,是绕不开的。其实在早期的 模型中,就已经明确涉及了“嵌入式技术进步”的概念。早在1962年,肯尼思·阿罗(Kenneth Arrow)在探讨经验积累与技术进步的关系时,就大胆根据资本品必然与生产伴随的观察,采用资本存量作为经验累积的一个间接测量。阿罗假定新的资本品总是比旧的资本品带来的产量高,这里面就蕴含了“嵌入式技术进步”的概念。
然而,阿罗的侧重点在于“干中学”(learning by doing),在他的模型里,技术进步是资本存量的函数,资本存量是生产经验的一个测度,生产经验的多少决定了技术进步的快慢,因为知识是在生产活动中产生的。而且,阿罗在文中也指出,他仅仅考察了在生产资本品过程中的学习和知识累积,没有考虑在使用资本品过程中的学习和知识积累,而后者其实对于发展中国家具有重要的意义:发展中国家通过购买资本品,与自己的劳动力结合,可以大幅促进自己的技术进步和人力资本积累。
其实,在函数形式上, 模型可以完全包含投资中嵌入技术进步这一思想。只可惜,阿罗着眼于“干中学”这一技术进步的方式,而不是资本积累包含技术进步这一思想。究其原因,视角不同可能是一个重要考量。阿罗的着眼点,更多是一个先进国家在技术前沿上的技术进步,而不是一个落后国家的学习和进步。

经济增长的文献,立足点往往在于长期的经济增长,实证的证据也大多来自欧美发达国家。对于这些国家而言,因为已经处于经济发展和技术进步的前沿,发展的核心动力来自技术进步,经济增长的模式是技术进步导致产出增加,带动投资增加,技术进步是源头。而对于落后国家而言,因为没有处于技术前沿,在追赶发达经济的过程中,一个重要的途径就是“进口”已有的技术,而这种进口,往往是通过投资实现的,发展的模式是投资增加带动技术进步,导致产出增加,这里投资增加是源头,与发达国家的经济增长模式有着很大的不同。这一不同,研究发展中国家经济追赶时不可不予以考虑。
[13] 代表性的内生增长模型包括AK模型(Arrow (1962), Frankel (1962), Romer (1986), Lucas (1988)),产品多样性模型(Romer (1987, 1990)),和熊彼特类型模型(Aghion和Howitt (1992))。
4
计量关系与因果关系
对于“过度投资”不可持续的另外一个更直接的回应,来自计量经济学家。认真修习过计量的人,都会明白一点:计量关系永远不能被解读为因果关系。计量关系本质上是变量之间的相关关系,不管是根据简单的简约化模型(reduced form model)计算出来的简单相关,还是根据复杂的结构性模型(structure model)计算出来的复杂相关,都依然还是相关关系,而不是因果关系。
在解读计量结果时,学者们通常会把发现的相关关系与某种理论结合,说明实证发现支持了某种理论,而根据该理论,考察的变量之间存在某种因果关系。但是这里面有两个层次:一是证据支持了理论,二是该理论假定了某种因果关系。倘若把两个层次混淆,直接认为是“证据表明了因果关系”,就大错特错了。倘若一个计量证据可以证明或者证否一个理论,把两个层次合二为一在证据很强的情况下似乎也无伤大雅。遗憾的是,经济学上没有这样的证据,经济学上的证据往往都是很间接的,计量的结果最多只能在一系列的假设条件下提供一些支持或者不支持的证据,我们不断积累计量的证据来支持或者不支持某一理论,从来不能证明或者证否一个理论。实际上,经济研究的演化方式,是不断积累证据,然后修正理论,然后积累更多的证据,是一个不断演化的过程。
把这一层关于计量的讨论简单应用到增长核算上,一个结论跃然纸上:增长核算只是表明增长中的直接贡献因素是什么,但是并没有任何关于增长原因的论述,因而增长核算也就完全不能拿来做增长原因,特别是增长持续性的讨论。从“增长的直接贡献因素”到“增长原因”,这看似很小的一步之间,却有天壤之别。增长核算可能发现要素投入的增加,比如资本积累和劳动参与率的提高,可以几乎完全解释经济增长,但是这一结果却对增长的根本原因毫无涉及。比如说,这一核算结果没有回答一个最基本的问题:要素投入为何会增加?非洲资源也很丰富,为什么不大幅增加要素投入而促进经济增长?增长核算研究的是增长本身,而不是增长的原因,因而在从增长核算中解读增长的原因时,总要有一个引申、解读的过程,这一过程要非常小心。
8
结语:舒尔茨的批判
对索洛模型的缺点的最深刻分析之一,来自另一位诺奖得主西奥多·舒尔茨(Theodore W. Schultz)。在分析传统农业向现代农业的转变,以及由此而产生的经济增长时,舒尔茨强调了新的生产要素的重要性,发现农业技术的进步,其实就是新的生产要素不断被发明,并推广应用的过程[14] 。比如,培育新的适宜当地的品种,新的品质好的肥料,新的更好的机械,这些新的生产要素代表了是农业技术进步的本质。这些要素的发明和应用,推动了农业生产的进步,释放了农业劳动力,使得工业发展成为可能,也推动了经济增长。

谈到经济增长理论时,舒尔茨对索洛模型的方法论表示了担心,认为索洛模型过于重视综合生产函数(aggregate production function),忽视了具体的生产过程,特别是忽视了新的生产要素的重要性。舒尔茨特别担心的是,综合生产函数这种方法把技术进步置于一个“黑箱子”当中,掩盖了技术进步的实质,其实是不利于深入理解技术进步这一经济增长的核心概念的。
可惜的是,尽管舒尔茨早有批评,但是后来索洛模型还是愈发流行起来,对于后来的研究产生了深远的影响。综合生产函数尽管粗略,但是可以把生产用一个简单的函数形式来表达,是一个极为便利的方法。在真实与便利之间,现代经济分析似乎对于后者更加偏爱。为了便利,人们可以包容模型的弱点,甚至选择视而不见。
索洛本人,对于他的模型产生的误导,其实不无察觉。在1987年他自己的诺奖发言中,就提到了他自己在模型中的妥协,并强调他自己早就知道要素积累的重要性,早在1958年就提出了“嵌入技术进步”的概念。可惜,后来的经济增长理论的演化,依然大致沿着“总体生产函数”的路径,对于技术进步的具体过程,特别是发展中国家技术进步的特征,重视不够。一种理论一旦发明,人们就会根据自己的便利而选择使用,发明者本人也没有办法。这验证了中国的一句古话:开弓没有回头箭。
倘若只是几个书生在书斋里论道,对社会思维没有什么影响,那怎么说也都无伤大雅。然而,索洛模型对于人们的思维,以及政策制定,都产生了重要的影响,经济政策讨论中对于索洛残差的众多关注,就是明证。关注也就罢了,很多分析把索洛残差简单等价于技术进步,就很容易产生误导了。可惜的是,尽管西奥多·舒尔茨早已指出索洛理论的方法论弱点,而且他本人亦贵为诺贝尔经济学奖得主,他的观点却很少被人提及,不禁令人唏嘘。