
小学数学练习机寻求线下独家代理,今天在广西桂林发展了一个线下代理。欢迎培训机构,小学老师,热爱营销人士独家代理你当地的线下销售权。如果你成为代理,我们会为你做一个只有你的联系方式的试用版软件。有意者请联系软件作者QQ 873979231。www.iibaby.net下载试用版。宝宝爱儿歌的安卓手机版已经做好了,下载网址是http://www.iibaby.net/erge.apk下载到电脑上后,用数据线可以安装到手机里。近千儿歌有专业配音,儿歌文字随配音变色,是孩子识字和学习普通话的好帮手,有学龄前儿童的家长一定要试试哦。本应用所有功能完全免费,并且不需要访问网络就可以使用。

新加坡数学课本
新加坡的中小学数学课程一直在国际上备受推崇。在上海学生参加PISA考试之前,新加坡的数学成绩长久占据第一的位置,目前则连续两届位居第二,仅次于上海。
无论是教材还是课堂设计,新加坡中小学的“数学模式”都是全世界效仿的对象。今年2月,法国就有500所学校引进新加坡教材,翻成法文,在课堂上推广。目前,全世界已有超过40个国家及地区采用新加坡数学的课本进行教学,新加坡数学为何如此受到“欢迎”?
近日,外滩教育记者特地探访了上海新加坡国际学校,看看新加坡数学教学的法宝到底是什么。
Model-Drawing,把抽象问题变图形
国内外的很多小学基础教育会通过互动的模式让孩子能够触摸到物件,比如数苹果或是掰手指头等,然后将这个结果转换成抽象的数字。“但是他们都忽略了一个步骤,就是将其图片化,”新加坡国际学校小学部数学主任Frankie说,“增加这个步骤可以让学生能够有一个过渡的过程,更直观地解读问题。”
对此,新加坡开创了独特的“Model-Drawing”学习方法。“很多人都会好奇这种方法是什么,” Frankie说,“其实很简单,就跟我之前说的那样,Model-Drawing就是将抽象的问题变成方格的形式来解决,而美国人则把我们的这种方法称为Bar-Modeling。”
在新加坡数学的教学过程中,会逐渐出现一些Model-Drawing的方法,帮助学生一步步的解决问题。“我们在二年级就会引入了一些比较简单的加减Model,三年级开始就会开始出现一些复合型的,如我们在初中阶段会接触到的告诉你两数之和及两数之差从而得出这两个数字的未知数方程,”Frankie告诉记者,“很多比较具有难度的代数问题其实我们在小学阶段都已经通过Model有所接触了。”
他继续道,“我们用这个方法学习数学并不是为了能够让学生更早的接触难度较高的内容,而是希望这样的方法能够让他们对代数有一个基本的认知。——这其实是一种思维的模式,在有了这样的思维方式和基本认知之后,代数本身就会变得简单很多。”
如何Draw Models
说了那么多,不如通过具体的题目来学一学Model-Drawing!
在Model中数字的大小通过方块的长短来表示,并且大小一样的方块代表的是相同的数字。在进行Model的时候我们要注意几点:
首先,在进行绘图的时候一次只能针对一个信息进行处理;
其次,所有的题目的资料包括问题都要在Model中体现出来;
还有非常重要的一点,不一样的数字要在绘图中明显的表现出来,并且,特别是两个内容之中同样的数字要排列整齐。
而Model本身通过题目的种类被简单的分为:“加减法”、“乘除法”、“比较”及“复合型”四种,接下来我们依次讲一讲如何用这几种Model解决问题。
首先是“加减法模型”,该模型一般是以一个长条的形式来表现。
下面是一个简单的“加减法模型”例题:
“Adam had 9 stickers. His brother gave hime another 12 stickers. How many stickers does Adamhave altogether?”
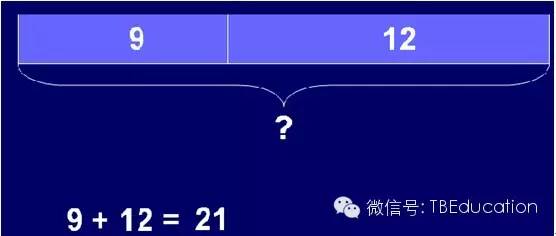
“很多家长都会误以为我们的这种方法是与中国的线段相类似的。其实不然,线段是将数字精确的标注出来,然后在上面进行计算得出结论,”Frankie说,“我们的这种Model不是一种类似代数这样的计算方法,而是在计算过程中用到的工具。”
在Model上并不是精确的表现所要计算的数字的大小和比例,只是简单的将其明显的区分开。“我们通过将题目中的各种条件整合在一个图片中宏观地解读问题,而后学生可以更快更清晰地解答问题。”
而新加坡数学中的乘除法模型则通过一个分为若干个部分的长条来体现:
这是二年级学生的乘法题目:
“Fang Ting counted 5 nests on a tree. There were 6 birds in each nest. Howmany birds were there altogether?”
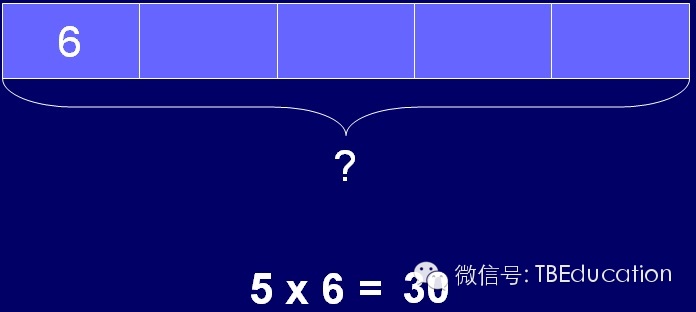
图中的5个方格即题目中的“5 nests”,而6即每个鸟巢的小鸟的个数,问号的部分就是需要求解的内容。“在进行乘除法这样会有很多方格的题目时,我们可以只标出一个方格的数字,在必要时可以将方格的数量用省略号表示,”Frankie提到,“有时候我们做除法的问题的时候,我们并不知道‘商’是什么,这个时候我们就可以用问号或者省略号来代替。”
相对简单的加减法和乘除法模型而言,比较型的模型相对更复杂,一般会有互相有比较的几个长条组成。有这样一个题目:
“Jane has 30 stamps more than Karen. They have a total of 64 stamps. How many stamps does Karen have?”
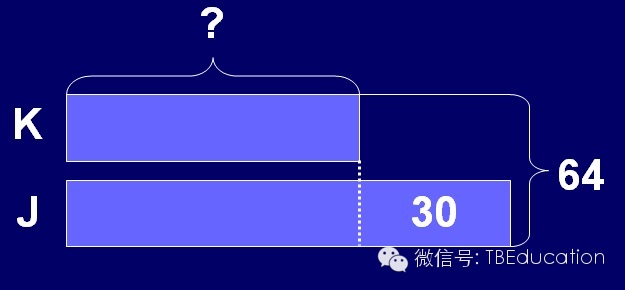
这其实是代数中非常基础但很重要的问题,也就是“x + y = 64, x – y= 30”。而三四年级的学生,在掌握了比较型的模型后,就可以开始解决这类问题了。“做这样问题的时候,我们教学的关键在于教会学生们把两个不知道的问题慢慢变成一个问题,”Frankie开始讲述教学的过程,“以这个问题为例,我们可以从Model中非常直观地看到K和J之间的比较,所以在第一步的时候就可以轻易的得出K+J的总数,从而得出结论。”
前几种简单的模型仅仅只是对Model-Drawing方法的入门,在解题中出现的较多的还是复合型模型,甚至可以说这是整个Model-Drawing教学中的“主力”。“并不是所有题目都是简单的加减乘除,很可能一个问题之中会出现各种运算方式,”Frankie告诉记者,“所以复合型的模型是我们会着重教学的点。”
我们可以看到这样一道题:
“Dawn’s basket contains 3 times as many oranges asNancy’s basket. After Dawn threw away186 rotten oranges and Nancy threw away 27 rotten oranges, Nancy had twice asmany oranges left as Dawn. How manyoranges were there in each girl’s basket at first?”
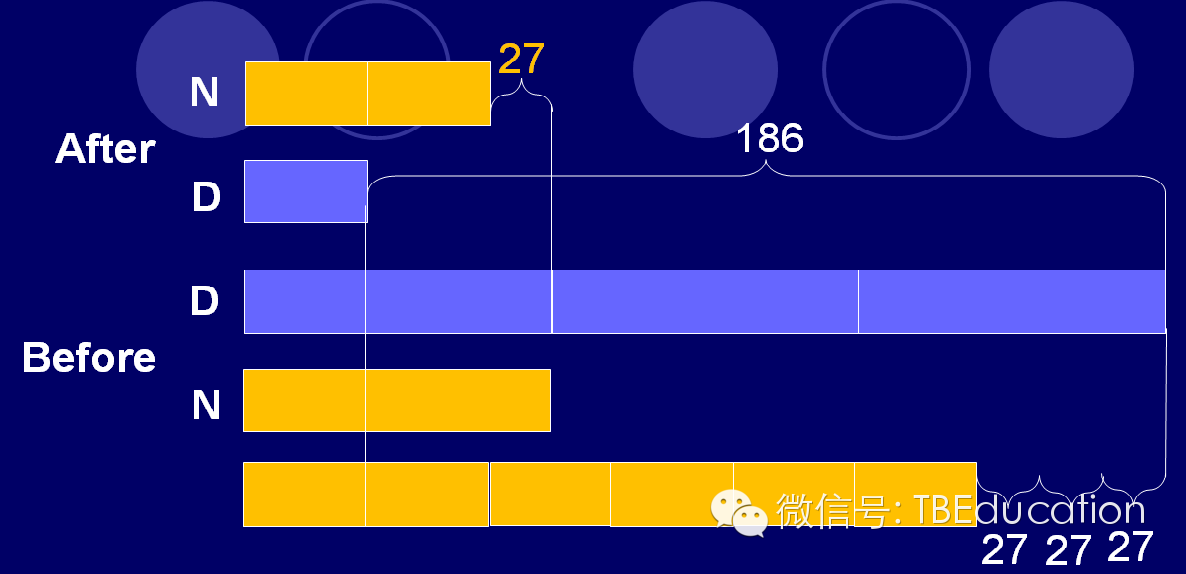
在做这样的题目时候,在教学中往往会建议学生优先画出最终的模型:即Nancy剩下的橘子比Dawn多两倍。之后再将在题目中所获得的信息画在自己的Model上,直观的看到整个题目的内容。在笔者看来,将题目中的条件“画出来”这样的步骤对一些简单的题目来说可能会有点“鸡肋”,——因为学生可以通过其他方式更快地解决一些问题,但遇到这样相对难度比较高的题目时,就会显得非常实用。
什么样的孩子适合Model-Drawing
作为新加坡数学教学的特色,Model-Drawing到底适不适合其他国家的学生,能否通用?Model-Drawing作为一种学习方法,可以说是锻炼孩子思维能力的一项工具。
“对于学习能力不是特别强的孩子来说,Model-Drawing可以帮助孩子在画图的过程中一步步地解读题目,”Frankie说,“在经过几年的锻炼之后,孩子看到题目之后会很自然的联想到这个方法,——很可能他并没有‘画出来’,但这种图片化的思维会让孩子的解题变得更快更轻松。”
不仅仅是学习能力不是特别强的学生,一些已经接触过代数的学生在学习了这种方法之后也更倾向于采用这样的方法解题。“我们学校的一些韩国学生在学习新加坡数学的同时,还会在周末参加韩式的数学课程,包括代数的学习,”Frankie告诉记者,“刚开始进Model-Drawing教学的时候他们也会出现排斥心理,认为可以通过代数的方法更简单的解决,但随着学习的深入,这些学生反而不会选择纯代数的解题。”
而作为学校小学部的数学主任,Frankie本身对这种方法也非常推崇,“我本身来自马来西亚,小时候也没有接受过这种课程化的Model-Drawing训练,”他说,“其实我自己也是在当老师的过程中边教边学,经过这么多年的教学,我也逐渐体会到这种图片化的模式带来的好处。而即便是对于一些中国学生来说Model-Drawing作为一种学习的工具,也是非常值得借鉴的。”