今天,我会对建模理论是如何运用在加减乘除四则运算和数学基本概念中的,进行全面讲解。这一部分比较简单,目的是让大家对建模理论有一个基本的认知,对之后我们利用该理论解决各种数学问题打下基础。先说一下大家比较关心的要不要买教材的问题。很多辅导机构和宝爸宝妈们推荐的教材,是新加坡一套比较经典的英文教材。这套教材在网上很容易可以搜得到,价格大概是200+RMB。



有教材的好处是知识点的表述更加循序渐进,并且配合了大量的练习题。而且教材是全英文的,很多家长认为学数学的同时,也能熟悉数学里常用的英文单词。但是,全英文的教材也对家长的英文能力提出了一定的要求。在小编看来,对于我们这次讲解的新加坡数学建模理论以及将来会讲到的珠心算,其实完全没必要买教材,也没必要报辅导班。只要大家精读我对建模理论的文章,配合我们上一篇文章中推荐的两个英文链接,足够轻松掌握这个理论,并教给我们的孩子。现在,我们就开始正式的讲解:一、加法例1:3 + 4 = ?画两个箱子,一个箱子表示3,另一个箱子表示4。加法模型有很多种画法,你可以选择孩子最喜欢的一种。画法一:
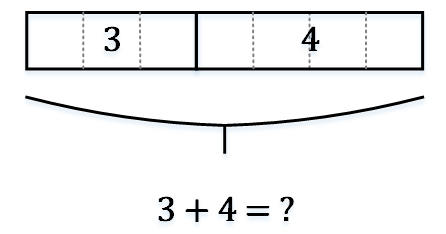
通过这个加法模型,我们把两个已知值“3”和“4”的箱子加起来,得到了未知值“?”。还有加法模型的其他画法如下:
画法二:
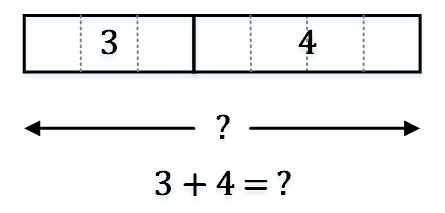
画法三:
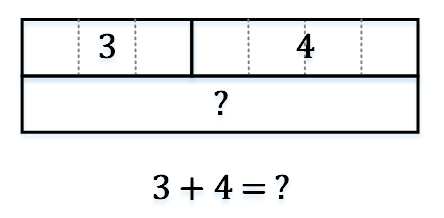
例2:两个以上的数相加
3 + 4 + 5 = ?
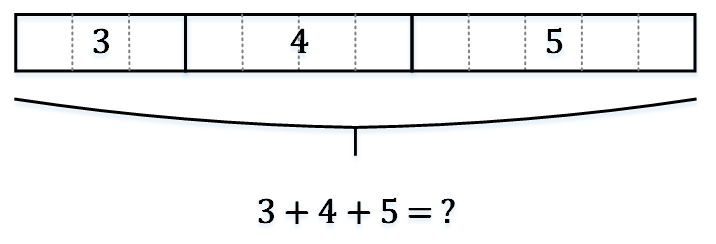
例3:学会给模型中的每个箱子命名
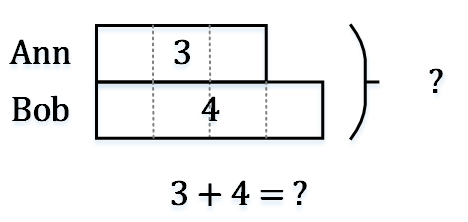
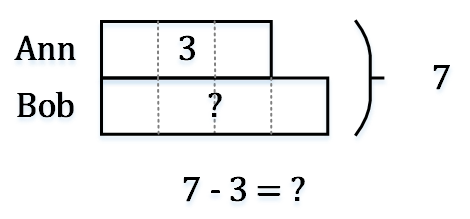
二、减法例1:7 – 3 = ?
画两个箱子,一个箱子表示7,另一个箱子表示3。减法模型有很多种画法,你可以选择孩子最喜欢的一种。
画法一:
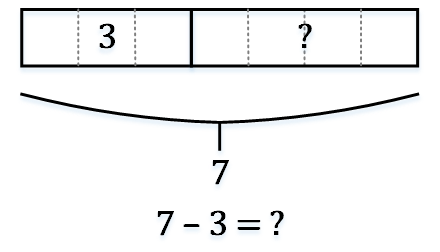
在这个模型中,从已知值为“7”的长盒子中拿去已知值为“3”的短盒子,得到未知值“?”。减法模型的其他画法如下:
画法二:
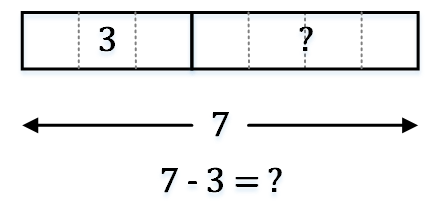
画法三:
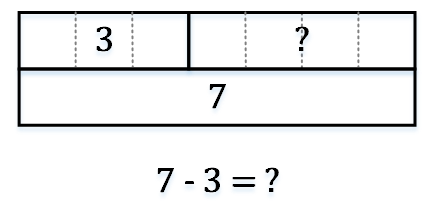
例2:减去两个数:12 – 3 – 4 = ?
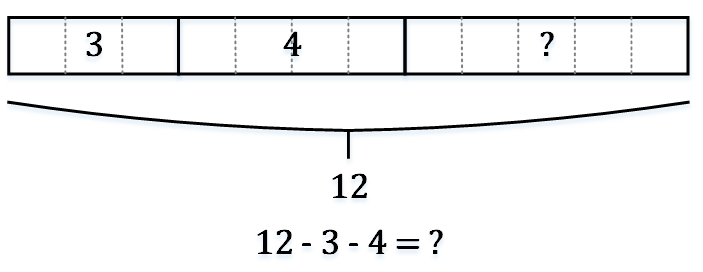
例3:学会给模型中的每个箱子命名:
三、乘法
例1:3 x 8 = ?画3个箱子代表3个组,每个组大小为8,乘法模型如下:画法一:
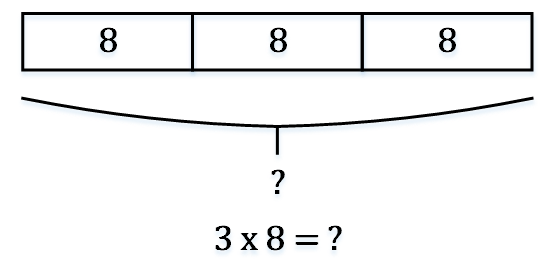
画法二:
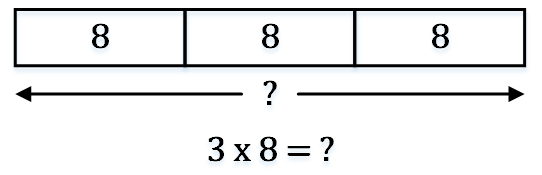
当组的数量太大时,仅仅需要画1个箱子表示第一个组,箱子右边跟随一个箭头,箭头末端表示组的数量。
例2:Ann有45包糖,每包8颗,请问Ann一共有多少颗糖?
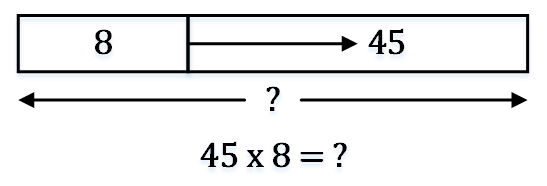
例3:学会对模型中的每个箱子命名
Ann有8个球,Bob的球是Ann的2倍。请问Bob有多少个球?
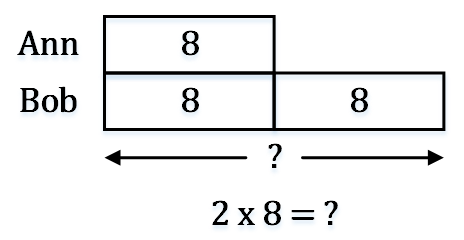
四、除法
例1:24 ÷ 3 = ?画3个箱子表示3个组,24表示3个组总共的数量。除法模型如下:画法一:
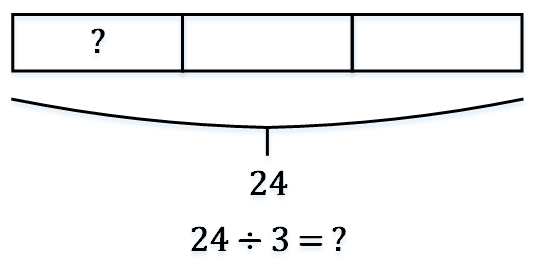
画法二:
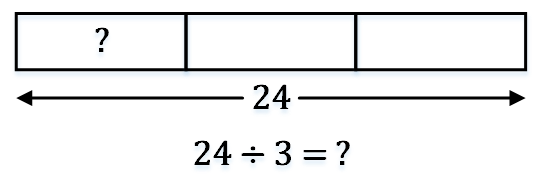
当组的数量太大时,可以只画一个箱子表示第一个组,箱子右边由一个箭头跟随,箭头末端的数字表示组的数量。
例2:Ann有360颗糖,她把它们平均放到45个小包里。请问每一个小包里有多少颗糖?
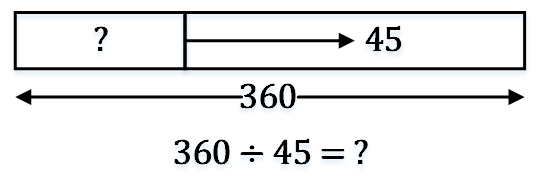
例3:Ann有360颗糖,她把它们平均分配到一些小包里,每个小包里8颗糖。请问,需要多少个小包装下这些糖?
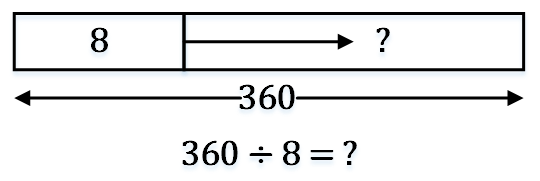
例4:学会为模型的每个箱子命名
Bob有16个球,Ann的球数是Bob的一半。请问Ann有多少颗球?
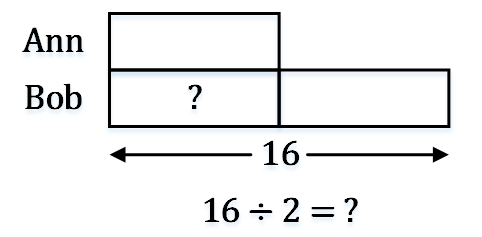
五、比较
“A比B多”模型
例1:21比17多多少
步骤1:画一个箱子,写“比”后面的数字17
步骤2:在箱子的右上角画一个点。这个点是下一步要画的箭头的起点
步骤3:从起点向右画一个的箭头(因为是“A比B多”模型)
步骤4:我们知道未知值“?”让已知值17更大。因此在箭头下面画第二个箱子,表示17被增大了“?”

步骤5:画最后一个箱子,等于前面两个箱子的长度,在这个箱子上写数字21。
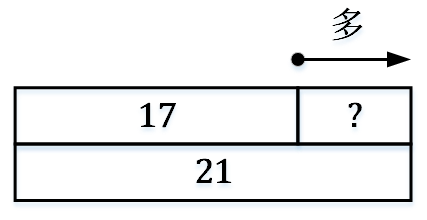
因此,21– 17 = 4“A比B少”模型
例2:多少比17少4?
步骤1:画一个箱子,写“比”后面的数字17
步骤2:在箱子的右上角画一个点。这个点是下一步要画的箭头的起点
步骤3:从起始点向左画一个箭头(因为是“A比B少”模型)
步骤4:我们事实上是要让已知值17小4。因此在箭头下面画第二个箱子,表示17被减小了4
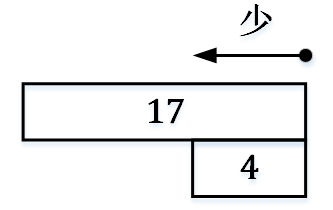
步骤5:在第二个箱子附近画最后一个箱子,使得三个箱子形成一个矩形,在这个箱子中写入未知值“?”
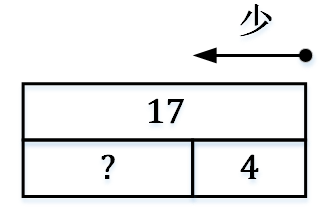
因此,17 – 4 = 13
六、分数
例1:一个数字的1/3是7,求这个数字
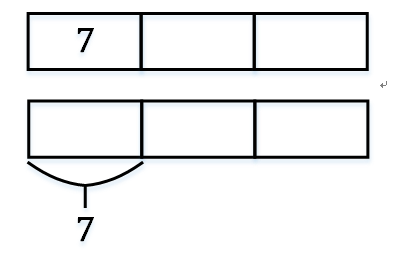
例2:一个数字的3/4是18,求这个数字
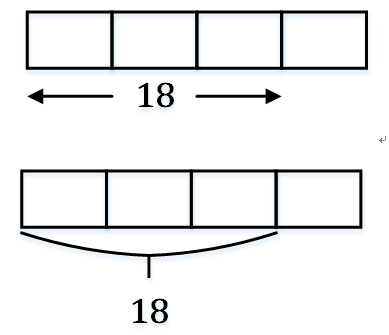
例3:Paul有30颗弹球,Paul弹球的4/5等于John弹球的2/3。John有多少颗弹球?
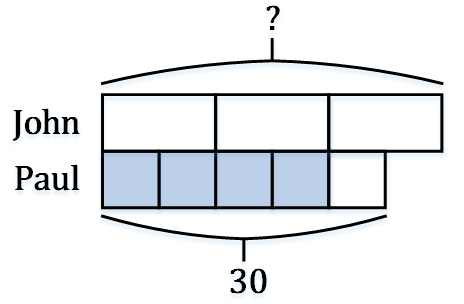
30 ÷ 5 = 6
6 × 6 = 36
七、百分数

例:Dan有28个贴纸,他拿走了25%,请问他拿走了多少?
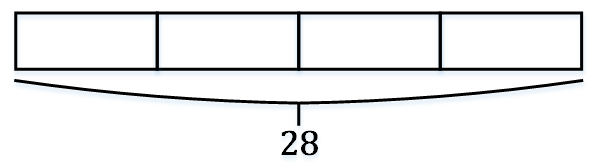
28 ÷ 4 = 7
八、小数
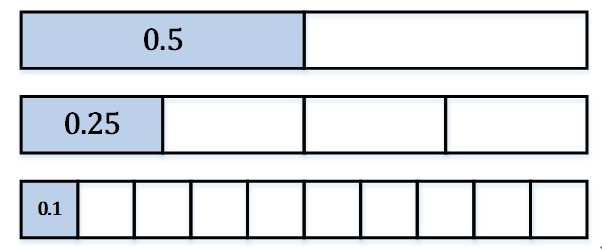
例:Lea有300本书,他拿走书的0.4倍,请问他拿走了多少本书?
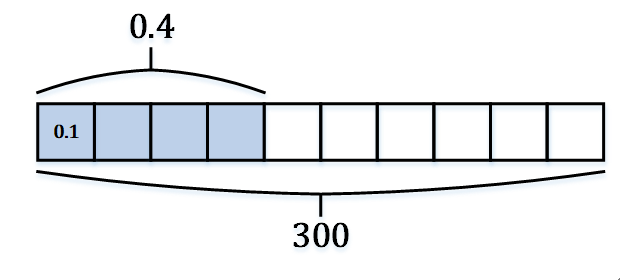
0.4 × 300 = 120
九、平均数
例1:找三个数的平均值。把三个数加到一起,用3除以这个总数。
模型画法一:
画法二:
例2:3个数的平均值是20,其中两个数是13和21,求第三个数的值?
3 × 20 = 60
60 – 13 = 47
47 – 21 = 26
十、比例
其中一项的值一定
例1:John有苹果和橘子数目的比例是3:8,如果苹果的数目是15,橘子的个数是多少?
15 ÷ 3 = 5
5 × 8 = 40
例2:John有苹果和橘子数目的比例是3:8,如果橘子的数目是40,苹果的个数是多少?
40 ÷ 8 = 5
5 × 3 = 15
两项的差值一定
例3:John有苹果和橘子数目的比例是3:8,如果橘子比苹果多25个,苹果的个数是多少?
25 ÷ 5 = 5
5 × 3 = 15
两项的总和一定
例4:John有苹果和橘子数目的比例是3:8,如果他总共有55个水果,苹果的个数是多少?
55 ÷ 11 = 5
5 × 3 = 15
至少有两项
例5:John有苹果和橘子和梨数目的比例是3:8:4,如果他总共有75个水果,苹果的个数是多少?
75 ÷ 11 = 5
5 × 3 = 15
到此为止,我们对数学中的四则运算和基本概念全部解析完毕,是对链接 http://www.teach-kids-math-by-model-method.com/ 中第一大板块Topic-matics的完整解读。如果为了阅读和打印方便,可以后台私信小编,索要电子版,拒绝任何商用目的。
上一篇:宝妈宝爸们在网上力荐的新加坡数学,真的很牛吗?